[10000印刷√] ピタゴラス の 定理 直角 三角形 351054

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

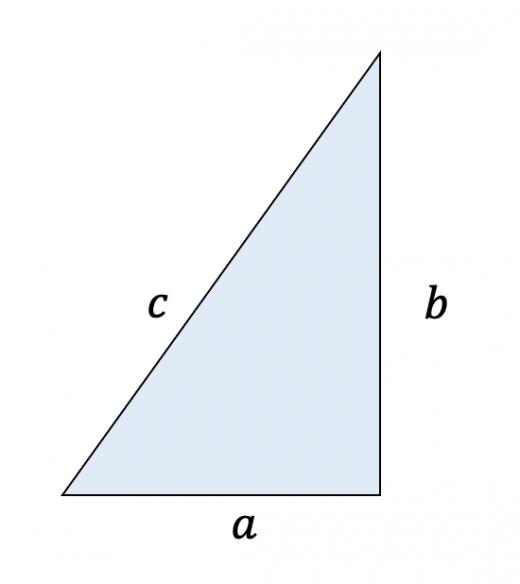
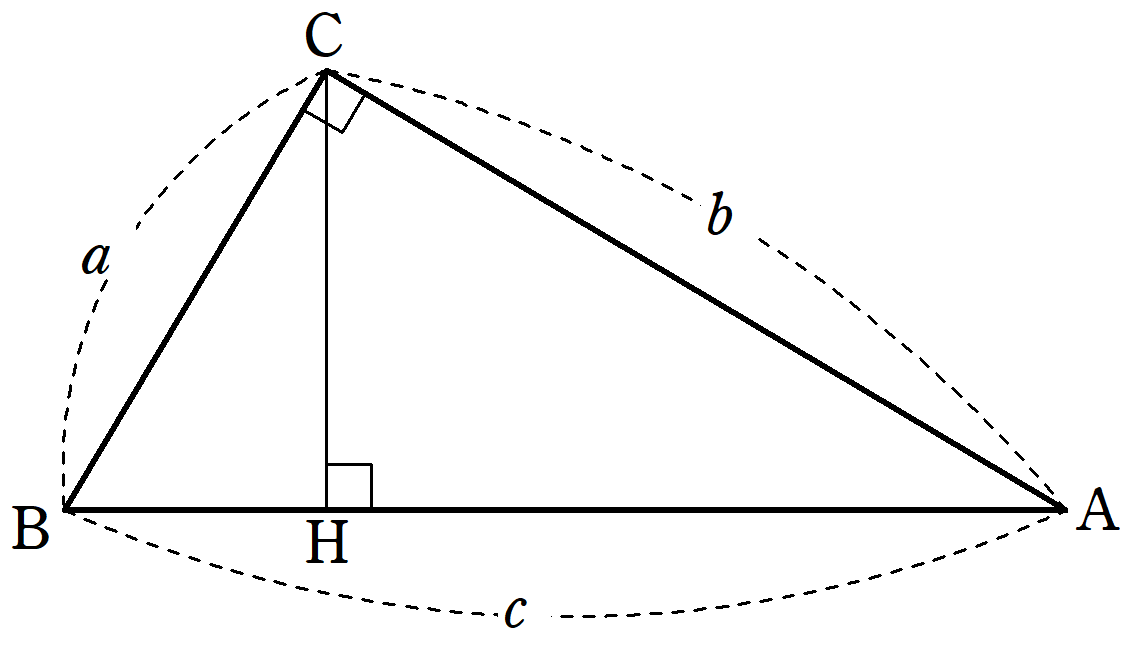
三平方の定理（ピタゴラスの定理） 三平方の定理は、直角三角形の3つの辺の長さの関係を表わした定理で、直角三角形の直角を挟む2つの辺の長さをそれぞれ a a 、 b b とし、斜辺の長さを c c とすると、 a2 b2 = c2 a 2 b 2 = c 2 の関係が成り立つ、という定理です。 つまり、三平方の定理は、 直角三角形の直角を挟む2つの辺の長さをそれぞれ2乗して足すと、その値は斜辺の長さを2乗したものあるピタゴラス三角形を拡大すると、新 しい直角三角形ができる。 新しくできた直 角三角形は、各辺が自然数であり、もとの 三角形に相似なので、これもまたピタゴラ ス三角形となる。 このようにあるピタゴラ ス三角形を2倍，3倍，4倍としていく と、次々に新たなピタゴラス三角形ができ る。 つまり、1つのピタゴラス三角形から 無数のピタゴラス三角形が生み出される。 これを記号で表現し

ピタゴラス の 定理 直角 三角形

ピタゴラス の 定理 直角 三角形-三平方の定理（ピタゴラスの定理） ∠ACB＝90°となる直角三角形ABCにおいて，各辺の長さを， BC= a BC = a ， CA = b CA = b ， AB =c AB = c とすると， a2b2 = c2 a 2 b 2 = c 2 の関係が成り立つ．この関係を 三平方の定理 あるいは ピタゴラスの定理 という． 中学受験ですので、三辺の 辺の比が整数となる直角三角形 がよく出題されます。 左側の $\textcolor{red}{345}$ の 三角形 は 超頻出 なので、覚えておいて欲しいですが、他の2つは そんなのもあるんだぁ~ 程度で良いかなぁ と 思います。

三平方の定理の証明 内接円を利用した証明方法をわかりやすく解説 面積と接線の性質をフル活用 Fukusukeの数学めも

 今回は、ピタゴラスの定理の逆、直角三角形となることの証明を紹介します。 ピタゴラスの定理とは、直角三角形の辺の長さ a,b,c a,b,c について、 a^2b^2=c^2 a2 b2 = c2 が成り立つことでした。 これは逆が成り立ちます。 どんな三角形であっても、辺の長さを a,b,c a,b,c として、 a^2b^2=c^2 a2 b2 = c2 が成り立つならば、その三角形は直角三角形となります。 これがピタ です。これは直角二等辺三角形の場合の三平方の定理ですね！ やはり、ピタゴラスは只者ではありません。 ちなみに、上のタイルを一般の直角三角形に応用した図は です。ここで面積が 大きな正方形＝小さな正方形＋直角三角形×4ピタゴラスの定理でわかる相対性理論 ―時空の謎を解く双曲幾何― ピタゴラスの定理がわかれば，球面幾何学の意味がすっきりし，双曲幾何学が手に取るようにわかります。さらに ピタゴラスの定理見方を変えて再度吟味してみると，球面

直角三角形の3辺の長さに関する a 2 b 2 =c 2 という関係はピタゴラスの定理（三平方の定理）と呼ばれます。 この定理はその名の通り古くから知られていますが、本当にピタゴラス(cBC570cBC500)が発見したかどうか確証があるわけではありません。初等幾何学 における ピタゴラスの定理（ ピタゴラスのていり 、 英 Pythagorean theorem ）は、 直角三角形 の3 辺 の長さの関係を表す。 斜辺 の長さを c, 他の2辺の長さを a, b とすると、定理は が成り立つという 等式 の形で述べられる 1 2 3 。 三平方の定理（ さんへいほうのていり ） 、 勾股弦の定理（ こうこげんのていり ） とも呼ばれる。 ピタゴラスの定理によって、直角三角形をなす3三平方の定理は、別名、 ピタゴラスの定理 とも呼ばれます。 三平方の定理（ピタゴラスの定理） 3 辺の長さが a, b, c の直角三角形 上の直角三角形において a2 b2 = c2 a 2 b 2 = c 2 が成り立つ 三平方の定理を使うと、 直角三角形の 2 つの辺の長さからもう一つの辺の長さを求めることができます 。 このページでは、三平方の定理を分かりやすく説明しています。 中学校で学習する前の人にも、

ピタゴラス の 定理 直角 三角形のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	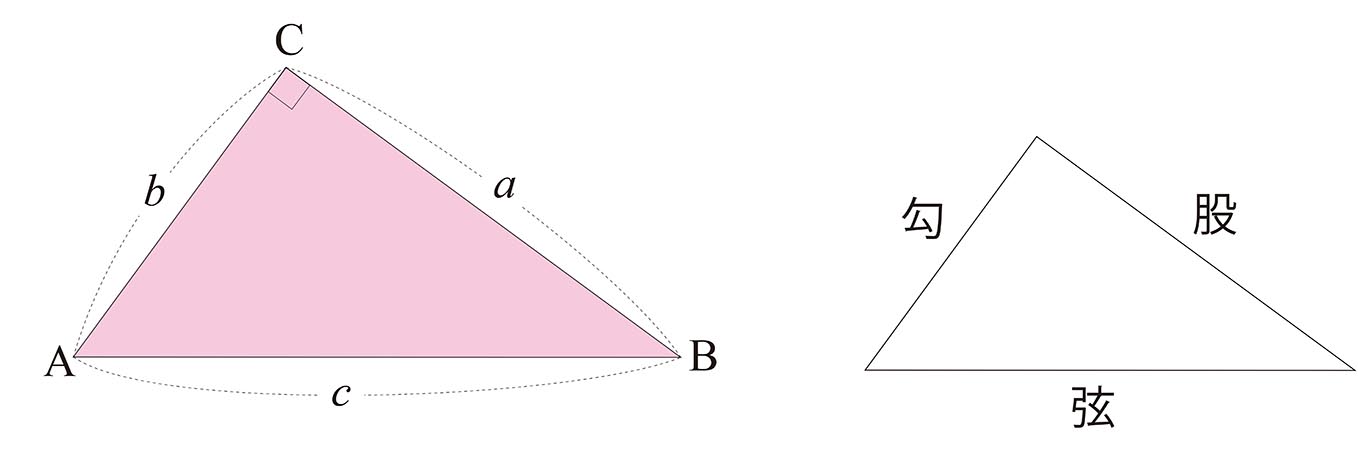三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	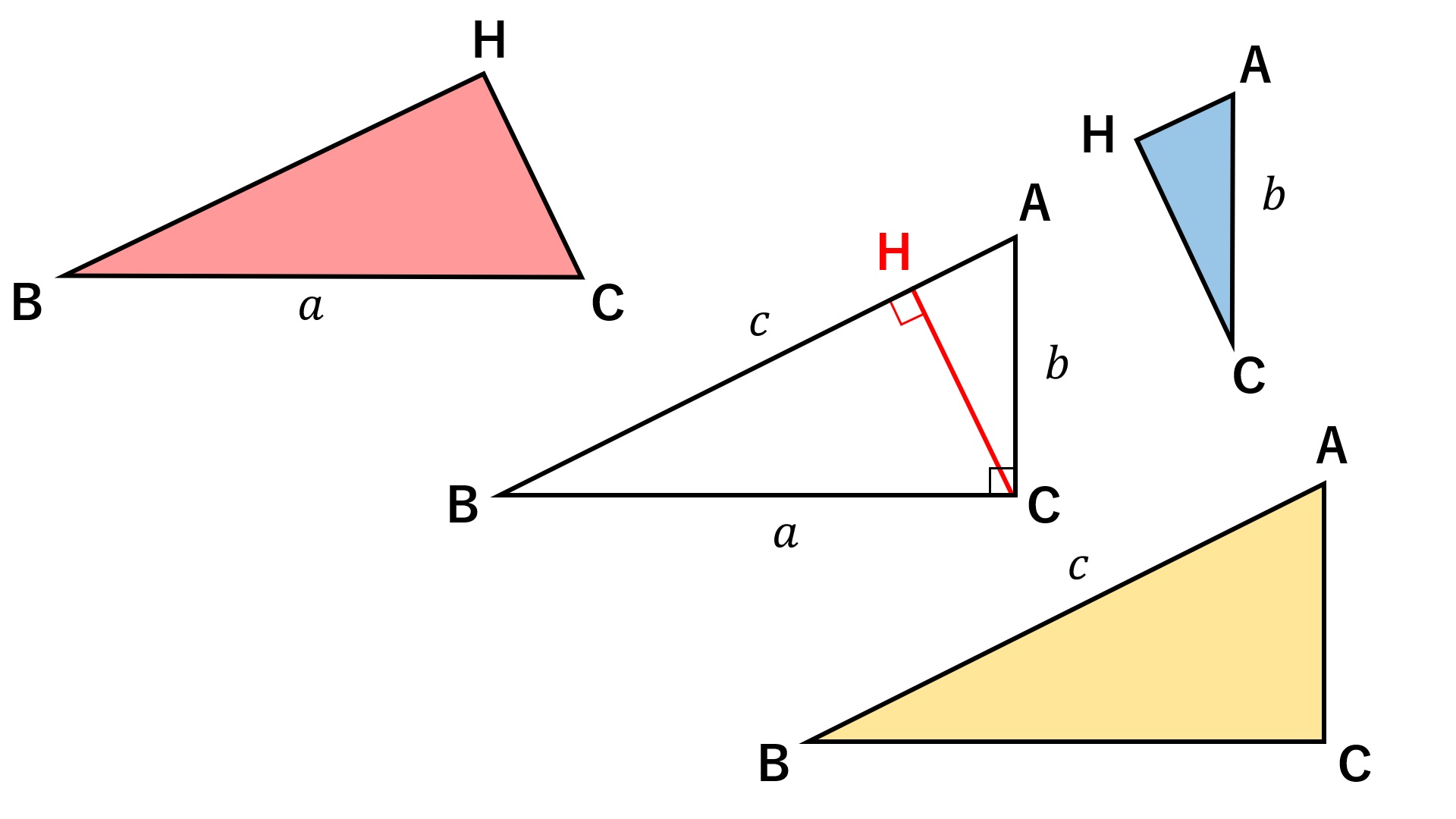三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	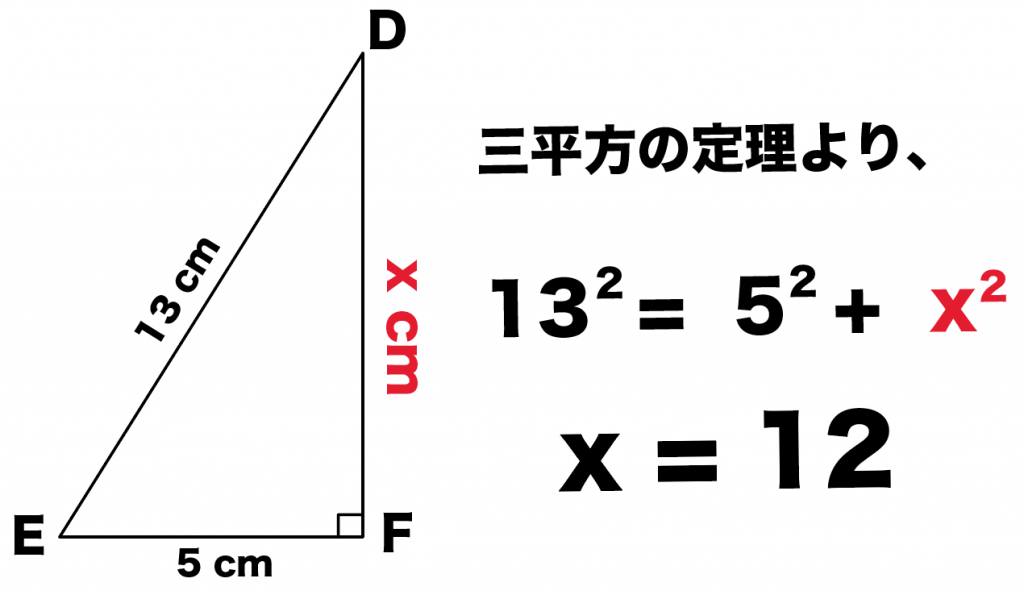三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	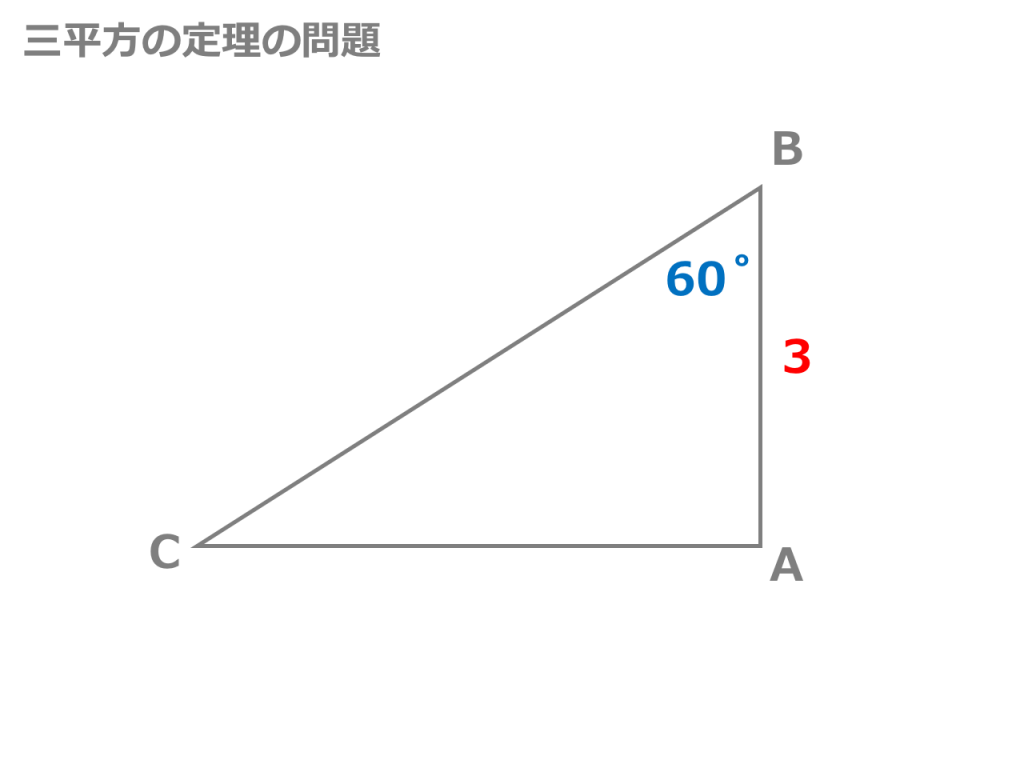三平方の定理の証明と使い方
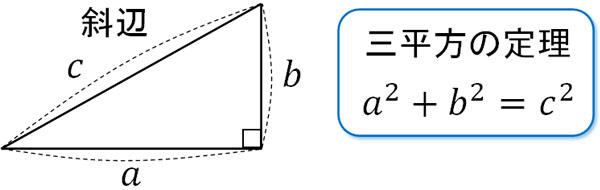三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	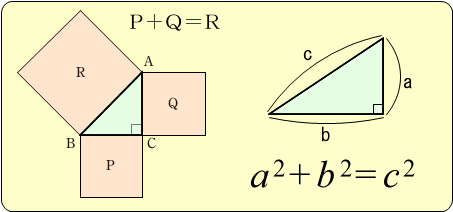三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	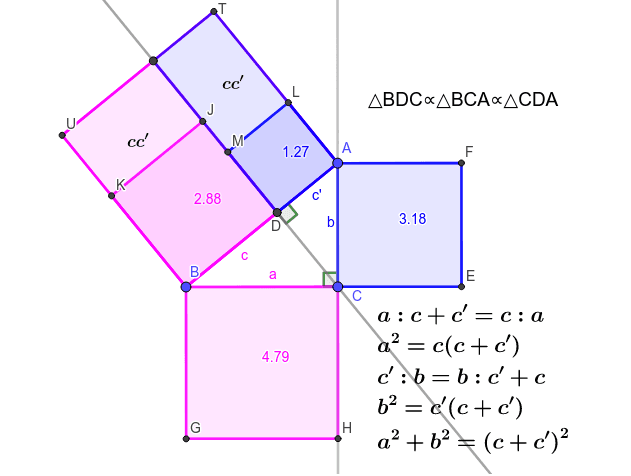三平方の定理の証明と使い方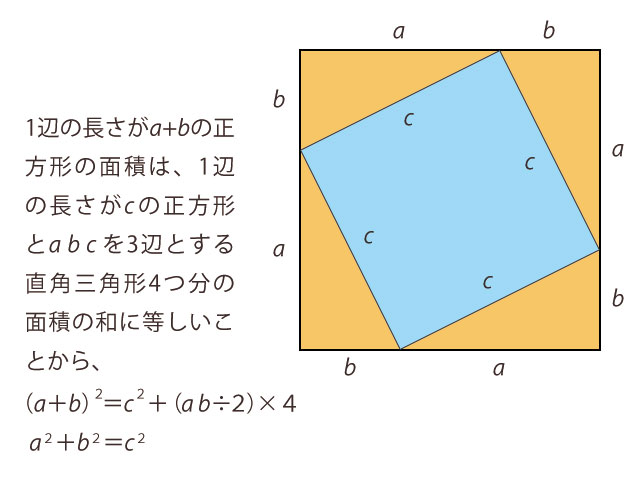
三平方の定理の証明と使い方	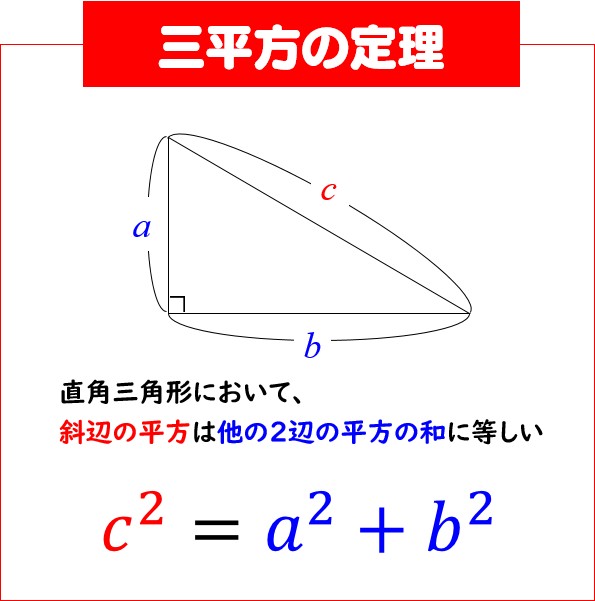三平方の定理の証明と使い方	三平方の定理の証明と使い方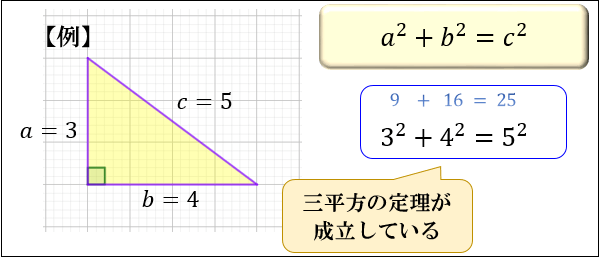
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	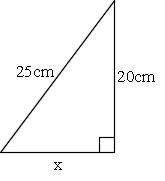三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	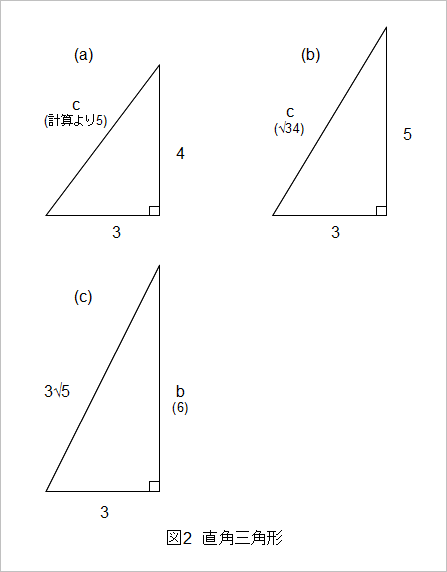三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	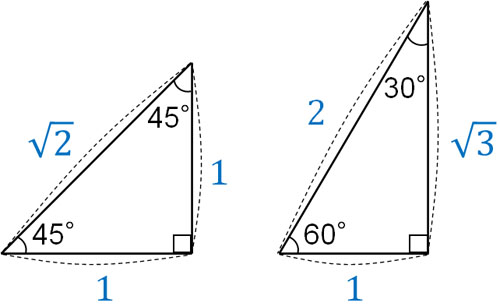三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	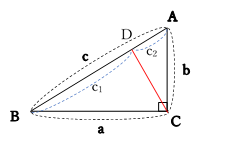三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	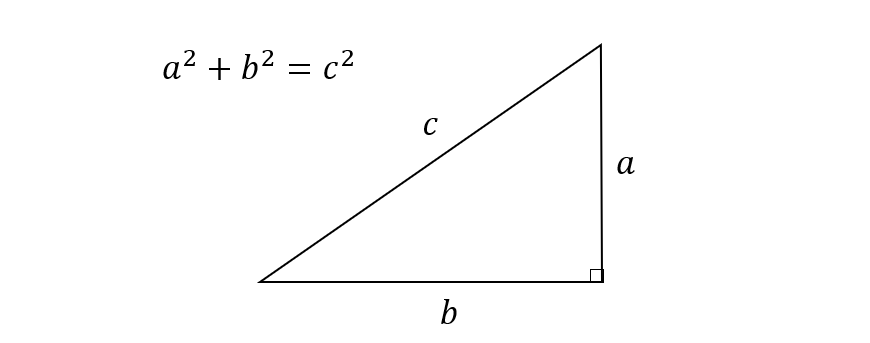三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方	三平方の定理の証明と使い方
三平方の定理の証明と使い方	三平方の定理の証明と使い方

 直角三角形の斜辺をc、他の二辺をa、bとすると、 青黄=緑 ピタゴラスさんが見つけたという話であるが、どうにも信憑性は薄い。 でも定理なんて有名になったもん勝ちなので私は別になんでも構わないが、最初に見つけた人は恐らく悔しからむ。 koichi さん 2135 ピタゴラスの定理自体は、直角三角形にしか使えませんが、 どんな三角形でも、2つの直角三角形に分割できます。 だから、直角三角形でない三角形でも、ピタゴラスの定理を使う場面はたくさんありますよ。 2人 がナイス！ して